08 - Steepest Descent Algorithm

21 Jun 2014 Comments

从前面几节中我们知道，各个优化算法的主要区别是如何构造 descent direction，这一节我们看看 steepest descent 如何构造 descent direction.

这一节画了很多 contour 的图，是通过这个脚本实现的

Steepest Descent Algorithm

Steepest Descent Algorithm 在每一轮迭代的过程中对函数做 affine approximation，也就是用一阶 taylor series 去近似 $f(\b{x})$

$f(\b{x}) \approx f(\b{x}^k) + f'(\b{x}^k)(\b{x} - \b{x}^k)$

然后通过优化这个近似函数得到 $\b{x}^{k+1}$

为了方便我们用 $f^k$ 表示 $f(\b{x}^k)$ ， $\b{g}^k$ 表示 $f’(\b{x}^k)$ ，另外注意到 $\b{x} - \b{x}^k$ 实际上就是我们要找的 $\b{d}^k$ ，这样上式就变成 $f(\b{x}^k) + {\b{g}^k}^T \b{d}^k$ 。因此 steepest descent 要解决的优化问题就是

$\underset{\b{d}^k}{\arg\min} \;\; f(\b{x}^k) + {\b{g}^k}^T \b{d}^k$

这里 $f(\b{x}^k)$ 是个 constant，可以从式子中去掉，另外，如果 $\b{d}^k$ 不做任何限制的话，它可以是一个无穷小的向量，这个近似函数就变成没有 lower bound，这样优化就没有意义了，所以我们限制 $\Vert \b{d}^k \Vert = 1$ ，这样最小化问题就变成了

$\begin{align*} \underset{\b{d}^k}{\arg\min} \;\; {\b{g}^k}^T \b{d}^k \\\\ s.t. \Vert \b{d}^k \Vert = 1 \end{align*}$

这个优化问题很好解

${\b{g}^k}^T \b{d}^k = \Vert \b{g}^k \Vert \Vert \b{d}^k \Vert \cos \theta = \Vert \b{g}^k \Vert \cos \theta$

当 $\theta = \pi$ 时这个式子最小，也就是 $\b{d}^k$ 和 $\b{g}^k$ 的夹角 $\pi$ 时上述近似函数值最小，如下图所示

上节中提到 $\b{d}^k$ 都可以表示成 $-A^k \b{g}^k$ ，对于 steepest descent， $A^k = I$ 。

Examples

现在让我们通过几个例子来看看 steepest descent 在不同情况下的表现

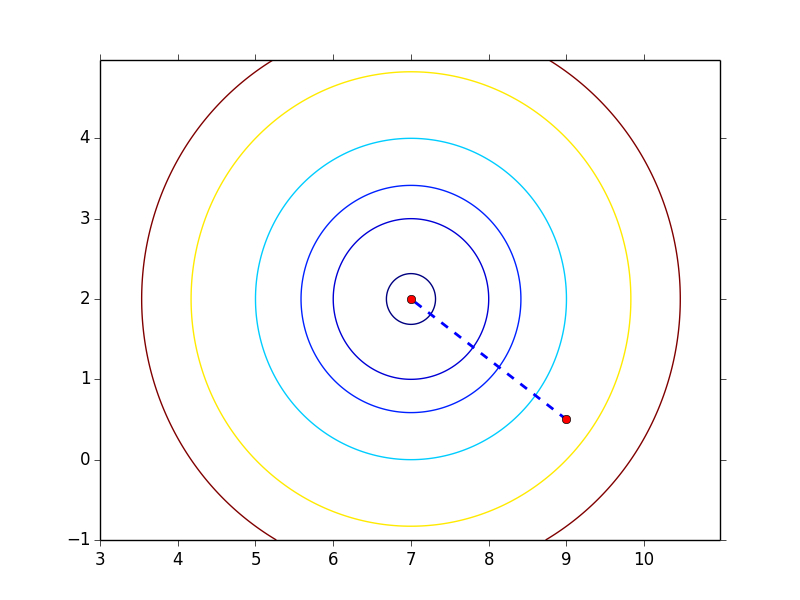
$f(\b{x}) = (\b{x}_1 - 7)^2 + (\b{x}_2 - 2)^2$

这个函数最优值在 (7, 2)，利用 steepest descent algorithm + exact line search，不论初始点选择在哪儿都是一步就能到最优点，如下图所示

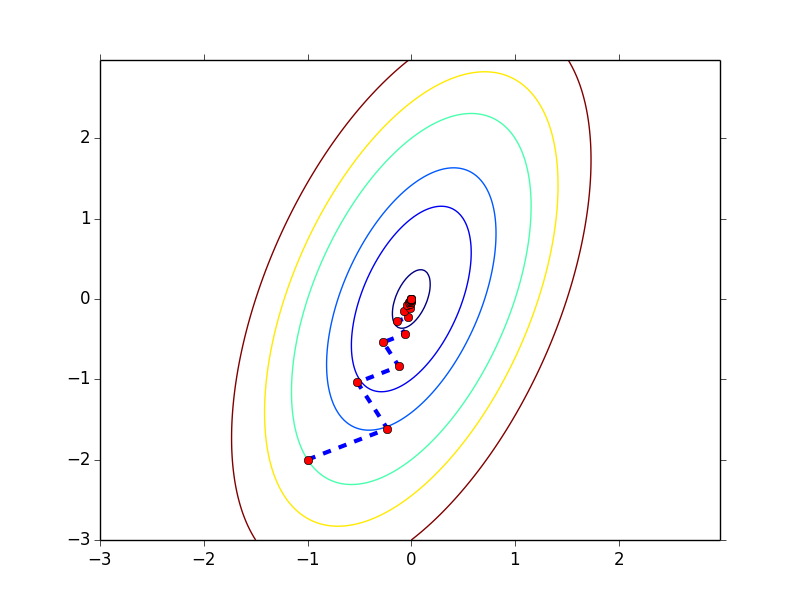
$f(\b{x}) = 4\b{x}_1^2 + \b{x}_2^2 -2\b{x}_1\b{x}_2$

这个函数的最优值点在 (0, 0)，同样我们用 steepest descent + exact line search

初始点为 (-1, -2)，函数的收敛过程如下图所示，以 0.001 为 gradient norm 的阈值，共迭代 27 步，实现见开头给出的脚本
初始点为 (1, 0)，函数的收敛过程如下图所示，以 0.001 为 gradient norm 的阈值，共迭代 5 步

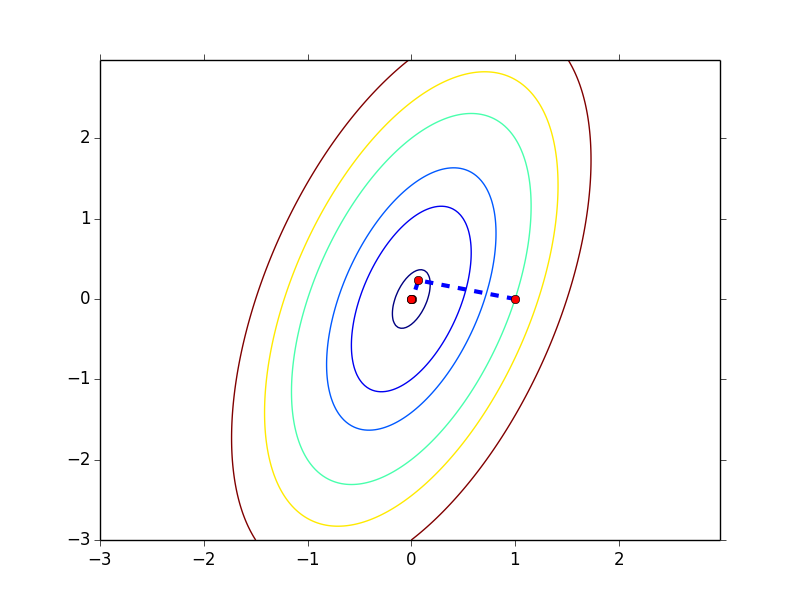
这个例子我们可以看出初始点的不同对收敛速度是有影响的

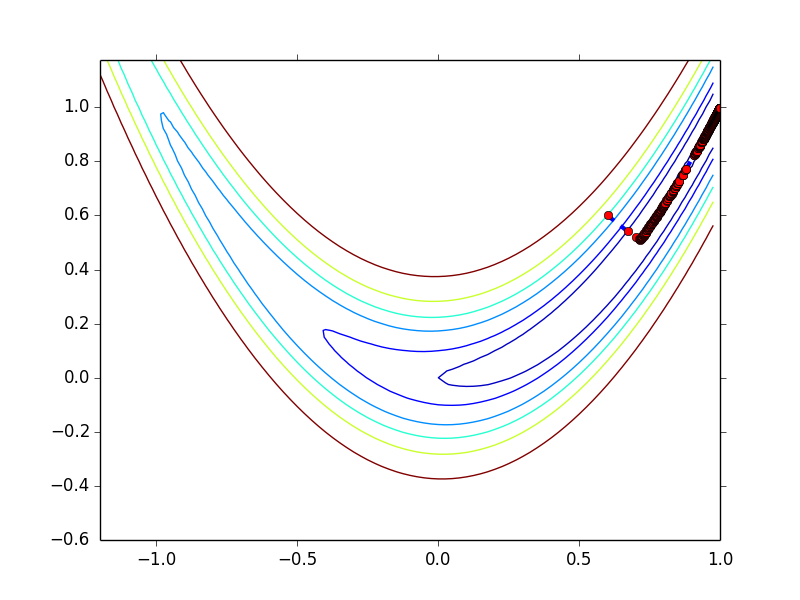
$f(\b{x}) = 100(\b{x}_2 - \b{x}_1^2)^2 + (1 - \b{x}_1)^2$

这个是著名的 Rosenbrock function，其最优值出现在 (1, 1) 点，利用 steepest descent + backtrack line search ( $\hat{\alpha} = 0.5, \lambda = 0.3, c_1 = 1\times 10^{-4}$ )

初始点为 (0.6, 0.6)，收敛过程如下图所示，以 0.001 为 gradient norm 的阈值，共迭代 2029 步
初始点为 (-1.2, 1)，收敛过程如下图所示，以 0.001 为 gradient norm 的阈值，共迭代 2300 步

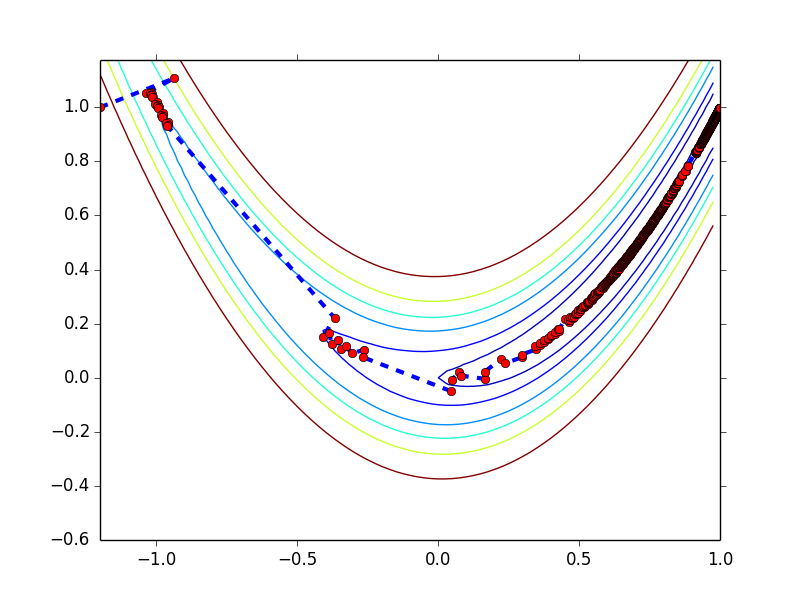
对于这个例子，不管你选那个初始点，迭代的过程总是很慢

上面的几个例子中，收敛的过程有快有慢，下面我们从理论的角度看看是什么导致了这种区别

Convergence Rate of Steepest Descent Algorithm

下面我们研究一下目标函数为 quadratic function $f(\b{x}) = \frac{1}{2}\b{x}^T H \b{x} - \b{c}^T \b{x}$ 时 steepest descent 的 convergence rate，其中 $H$ 是 symmetric positive definite matrix

关于 quadratic function 这里多说两句，其实 quadratic function 在很多情况下会成为研究重点，不单因为它简单，或者容易可视化，还有一个很重要的原因是，任何一个函数在接近 local minimum 的地方表现都和 quadratic function 相似，原因很简单，看 $f(x)$ 的 Taylor series 就知道了 $f(x) = f(x^*) + f'(x^*)(x - x^*) + \frac{1}{2}(x - x^*)^T H(x^*) (x - x^*) + O(\left\Vert x - x^* \right\Vert ^3)$ 其中 $x^*$ 表示 local minimum。从公式可知 $x$ 越接近 $x^*$ ， $\left\Vert x - x^* \right\Vert ^3$ 就越小，相应的 $f(x)$ 的行为也越接近于前面的 quadratic 的部分。所以研究 quadratic function 比看起来要重要得多。

由于 $H$ 是 symmetric positive definite matrix，所以我们可以直接得到这个函数的 close-form solution，只需令 gradient 等于 0 即 $\b{g} = H\b{x} - \b{c} = 0$ 可得

$\b{x}^* = H^{-1}\b{c}$

为了计算 convergence rate，这里定义 Error function $E(\b{x}^k) = \frac{1}{2}(\b{x}^k - \b{x}^*)^T H (\b{x}^k - \b{x}^*)$ ，并以

$\frac{E(\b{x}^k) - E(\b{x}^{k+1})}{E(\b{x}^k)}$

表示 convergence rate，注意到

$\begin{align*} E(\b{x}^k) = & \frac{1}{2}(\b{x}^k - \b{x}^*)^T H (\b{x}^k - \b{x}^*) \\\\ = & \frac{1}{2}(\b{x}^k H \b{x}^k - 2\b{x}^* H \b{x}^k + \b{x}^* H \b{x}^*) \\\\ = & \frac{1}{2} \b{x}^k H \b{x}^k - \b{c} \b{x}^k + \frac{1}{2}\b{x}^* H \b{x}^* \;\; (\because \b{x}^* = H^{-1}\b{c})\\\\ = & f(\b{x}^k) + \frac{1}{2}\b{x}^* H \b{x}^* \end{align*}$

其中 $\frac{1}{2} \b{x}^* H \b{x}^*$ 是个常量，所以 $E(\b{x})$ 和 $f(\b{x})$ 本质上是一样的。

展开 convergence rate，对于分子分母分别有

分子代入 $\b{x}^{k+1} = \b{x}^k - \alpha^k \b{g}^k$ 有
$\begin{align*} E(\b{x}^k) - E(\b{x}^{k+1}) = & \frac{1}{2} \b{x}^k H \b{x}^k - \b{c} \b{x}^k - \frac{1}{2} \b{x}^{k+1} H \b{x}^{k+1} + \b{c} \b{x}^{k+1} \\\\ = & {\alpha^k ({\b{x}^k} - {\b{x}^*})^T H \b{g}^k - \frac{1}{2}{\alpha^k}^2 {\b{g}^k}^T H \b{g}^k} \\\\ = & {\alpha^k (H \b{x}^k - c)^T \b{g}^k - \frac{1}{2}{\alpha^k}^2 {\b{g}^k}^T H \b{g}^k} \\\\ = & {\alpha^k {\b{g}^k}^T \b{g}^k - \frac{1}{2}{\alpha^k}^2 {\b{g}^k}^T H \b{g}^k} \\\\ \end{align*}$
对于分母，由于 $H(\b{x}^k - \b{x}^*) = H\b{x}^k - c = \b{g}^k$ 有
$\begin{align*} E(\b{x}^k) = & \frac{1}{2}(\b{x}^k - \b{x}^*)^T H (\b{x}^k - \b{x}^*) \\\\ = & \frac{1}{2} {(H^{-1}\b{g}^k)}^T H (H^{-1}\b{g}^k) \\\\ = & \frac{1}{2} {\b{g}^k}^T H^{-1} \b{g}^k \end{align*}$

这样 convergence rate 就变为

$\frac{2 \alpha^k {\b{g}^k}^T \b{g}^k - {\alpha^k}^2 {\b{g}^k}^T H \b{g}^k}{ {\b{g}^k}^T H^{-1} \b{g}^k}$

假设我们使用 exact line search，易推出 $\alpha^k = \frac{ {\b{g}^k}^T\b{g}^k}{ {\b{g}^k}^T H \b{g}^k}$ ，代入上式得

$\frac{E(\b{x}^k) - E(\b{x}^{k+1})}{E(\b{x}^k)} = \frac{({\b{g}^k}^T \b{g}^k)^2}{({\b{g}^k}^T H \b{g}^k)({\b{g}^k}^T H^{-1} \b{g}^k)}$

为了给上式一个 lower bound，我们引入 Kantorovich inequality

Let $H \in \mathbb{R}^{n\times n}$ be a symmetric positive definite matrix. Let $\lambda_1$ and $\lambda_n$ be respectively the smallest and largest eigenvalues of $H$ . Then, for any $\b{x} \neq 0$ $\frac{(\b{x}^T \b{x})^2}{(\b{x}^T H \b{x})(\b{x}^T H^{-1} \b{x})} \geq \frac{4\lambda_1 \lambda_n}{(\lambda_1 + \lambda_n)^2}$

根据 Kantorovich inequality，我们有

$\frac{E(\b{x}^k) - E(\b{x}^{k+1})}{E(\b{x}^k)} \geq \frac{4\lambda_1 \lambda_n}{(\lambda_1 + \lambda_n)^2}$

等价于

$E(\b{x}^{k+1}) \leq (\frac{\lambda_n - \lambda_1}{\lambda_n + \lambda_1})^2 E(\b{x}^k)$

因此根据我们定义的 $E(\b{x})$ ，steepest descent 是一个 convergence rate $\leq (\frac{\lambda_n - \lambda_1}{\lambda_n + \lambda_1})^2$ 的 linear convergence algorithm.

对 convergence rate 做个简单的变形

$(\frac{\lambda_n - \lambda_1}{\lambda_n + \lambda_1})^2 = (1 - \frac{2}{\frac{\lambda_n}{\lambda_1} - 1})^2$

其中 $\frac{\lambda_n}{\lambda_1}$ 表示一个 matrix 的 condition number，可以看出 condition number 越大，convergence rate 越大，算法收敛得越慢。当 $\lambda_1 = \lambda_n$ 时，收敛是最快的，对应上面例子中 circular contour 的情况，condition number 越大，contour 越扁，越小 contour 越圆。

结论

从上面的例子和理论分析中，可以得出如下结论

收敛速度确实和初始点的选择有关
Steepest descent 是一个 linear convergence algorithm，并且收敛速度取决于 Hessian matrix 的 condition number，condition number 越大收敛越慢
对于 nonquadratic function，上面的结论也是可用的，前面已经讲过，在接近 local minimum 的地方，任何函数的表现都可以用 quadratic function 近似，因此 nonquadratic function 的 convergence rate 取决于 $H(\b{x}^) $的 condition number，其中$ \b{x}^$ 是 local minimum

改进 Steepest Descent

假设要优化的函数是 quadratic function $f(\b{x}) = \frac{1}{2} \b{x}^T H \b{x} - \b{c}^T \b{x}$ ，其中 $H$ 是 symmetric positive definite matrix。

前面已经提到 $H$ 的 condition number 对收敛速度的影响非常大，condition number 越小，收敛得越快，当 $H = I$ 时收敛最快。由此产生的一个优化思路是，对原始 function 做空间变换，使其在新空间中的 Hessian matrix 为 $I$ ，然后在新空间中做优化，再将结果映射回原始空间，这样迭代就可以一步完成。

假设原始空间为 x-space，新空间为 y-space，则我们试图找到的变换是

$f(\b{x}) = \frac{1}{2} \b{x}^T H \b{x} - \b{c}^T \b{x} \; \Rightarrow \; h(\b{y}) = \frac{1}{2} \b{y}^T \b{y} - \b{c}_y^T \b{y}$

参考下图

由于这里 $H$ 是 symmetric positive definite matrix，这个变换可以通过对 $H$ 做 Cholesky decomposition 实现，如下

$f(\b{x}) = \frac{1}{2} \b{x}^T H \b{x} - \b{c}^T \b{x} = \frac{1}{2} \b{x}^T L L^T \b{x} - \b{c}^T \b{x} = \frac{1}{2} (L^T \b{x})^T (L^T \b{x}) - \b{c}^T \b{x}$

令 $\b{y} = L^T \b{x}$ ，则有

$h(\b{y}) = \frac{1}{2} \b{y}^T \b{y} - (L^{-1} \b{c})^T \b{y}$

这样我们就实现了通过空间变换得到一个 Hessian matrix 为 $I$ 的 quadratic function。在 $h(\b{y})$ 应用 steepest descent 有 (令 $\alpha = 1$ )

$\b{y}^{k+1} = \b{y}^k - \nabla h(\b{y}^k) = \b{y}^k - (\b{y}^k - L^{-1}\b{c}) = L^{-1}\b{c}$

所以无论你从什么初始点开始，都是一步到达 global minimum，把这个点映射回 x-space，得 $\b{x}^{k+1} = L^{-T}L^{-1} \b{c} = H^{-1}\b{c}$

这就是在 x-space 的最优解。

如果我们将 y-space 的迭代步骤映射到 x-space 的话是这样

$\begin{align*} & \b{y}^{k+1} = \b{y}^k - \nabla_{\b{y}^k} h(\b{y}^k) \\\\ \Longleftrightarrow & L^{-T}\b{y}^{k+1} = L^{-T}\b{y}^k - L^{-T}\nabla_{\b{y}^k} f(L^{-T} \b{y}^k) \\\\ \Longleftrightarrow & \b{x}^{k+1} = \b{x}^k - L^{-T} L^{-1} \nabla f(\b{x}^k) \\\\ \Longleftrightarrow & \b{x}^{k+1} = \b{x}^k - H^{-1} \nabla f(\b{x}^k) \\\\ \end{align*}$

这最后一步实际上是 Classical Newton 的迭代步骤。但要注意 Classical Newton 并不是由 Steepest Descent 演化过来的，实际上，二者的发明并没有什么联系，并且 Classical Newton 出现比 Steepest Descent 还要早得多，下一片文章我们将看到 Classical Newton 是基于什么思想得到的。