09 - Classical Newton Method

05 Jul 2014 Comments

这一节画了很多 contour 的图，是通过这个脚本实现的

Classical Newton Method

Classical Newton 基于的思想是在每步迭代的过程中对函数做 quadratic approximation，也就是用二阶 taylor series 去近似 $f(\b{x})$

$$f(\b{x}) \approx f(\b{x}^k) + g^T(\b{x}^k)(\b{x} - \b{x}^k) + \frac{1}{2} (\b{x} - \b{x}^k)^T H(\b{x}^k) (\b{x} - \b{x}^k)$$

然后通过优化这个近似函数得到 $\b{x}^{k+1}$，为了方便，后面以 $\b{g}^k$ 表示 $g(\b{x}^k)$，以 $H^k$ 表示 $H(\b{x}^k)$。

优化这个 quadratic approximation 并不复杂，令其导数为 0 即 $\b{g}^k + H^k (\b{x} - \b{x}^k) = 0$ 可得

$$\b{x}^{k+1} = \b{x}^k - {H^{k}}^{-1} \b{g}^k$$

之前已经说过每步迭代的 descent direction 可以表示为 $\b{d}^k = -A^k \b{g}^k$，对于 Classical Newton，$A^k = {H^{k}}^{-1}$，另外注意到，传统的 Classical Newton 并不设 step length，也就是 step length 统一设为 1，当然你也可以在每步做 line search。

下图给出 Rosenbrock function $f(\b{x}) = 100(\b{x}_2 - \b{x}_1^2)^2 + (1 - \b{x}_1)^2$ 在点 $(-0.5, 0)$ 处的 quadratic approximation，其中红点表示 $(-0.5, 0)$，绿色的 contour 就是 quadratic approximation 对应的 contour

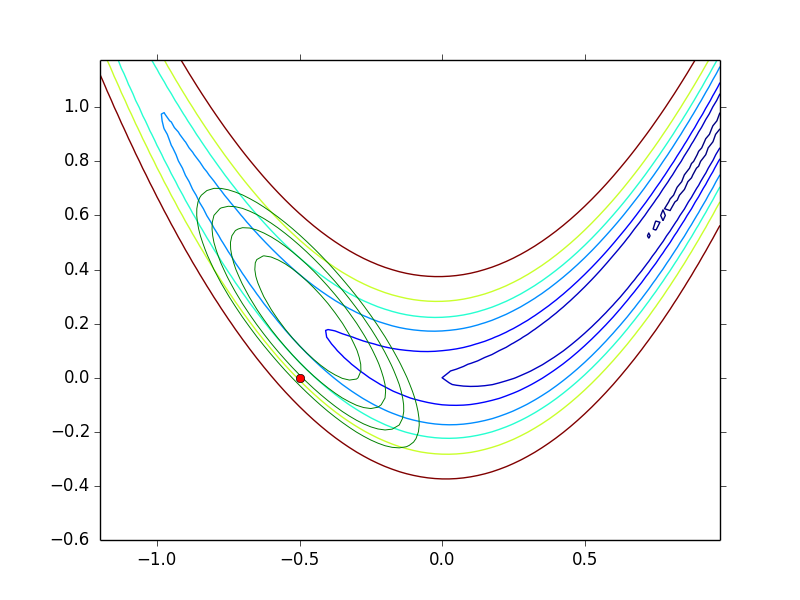
注意到如果你的函数本身就是个 quadratic function $f(\b{x}) = \frac{1}{2} \b{x}^T H \b{x} - \b{c}^T \b{x}$，则无论初始点选在哪儿，Classical Newton 都可以一步收敛到最优解

$$\b{x}^1 = \b{x}^0 - H^{-1} (H\b{x}^0 - \b{c}) = H^{-1}\b{c}$$

Examples

还用 steepest descent 中给出的例子

$f(\b{x}) = (\b{x}_1 - 7)^2 + (\b{x}_2 - 2)^2$ 和 $f(\b{x}) = 4\b{x}_1^2 + \b{x}_2^2 -2\b{x}_1\b{x}_2$

对于这两个 case，无论你初始点设在哪里，Classical Newton 都是一步即可收敛

$f(\b{x}) = 100(\b{x}_2 - \b{x}_1^2)^2 + (1 - \b{x}_1)^2$

其最优值出现在 (1, 1) 点，利用 Classical Newton + backtrack line search ($\hat{\alpha} = 1, \lambda = 0.3, c_1 = 1\times 10^{-4}$)

• 初始点为 (0.6, 0.6)，收敛过程如下图所示，以 0.001 为 gradient norm 的阈值，共迭代 10 步

  

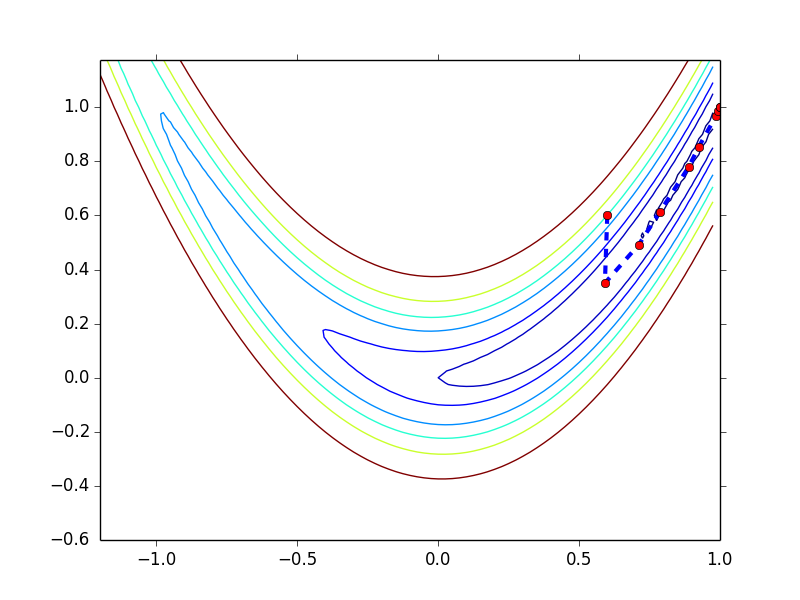
• 初始点为 (-1.2, 1)，收敛过程如下图所示，以 0.001 为 gradient norm 的阈值，共迭代 21 步

  

---

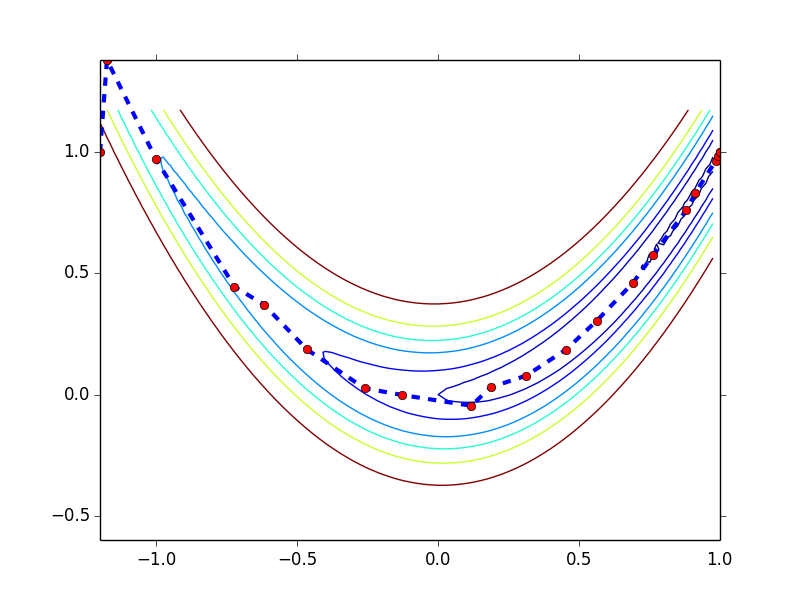
从这几例子可以看出，对比 steepest descent，Classical Newton 收敛所需的步数要少了很多。

Classical Newton 的问题

• 计算 $\b{d}^k = -{H^k}^{-1} \b{g}^k$ 是一个非常费资源的操作，由于 invert matrix 是一个 numerically unstable 的操作，所以通常转化为对 linear system $H^k \b{d}^k = -\b{g}^k$ 的求解，但这一求解还是需要需要 $O(N^3)$ 的计算和 $O(N^2)$ 的存储，所以依然是个非常费资源的操作

• 没法保证 $H^k$ 每步都是可逆的，$H^k$ 可能接近一个 singleton matrix，这会导致它非常难于 invert

• $H^k$ 也不一定是 positive definite matrix，这就导致 $\b{d}^k$ 可能不是 descent direction

• 没有做 line search，不保证 $f(\b{x}^{k+1}) < f(\b{x}^k)$

• 对初始点敏感，根据你初始点选择的不同，Classical Newton 可能不收敛

  考虑一个一维的 case $f(x) = \log(e^x + e^{-x})$

  • 如果初始点是 1，迭代收敛

  • 如果初始点是 1.1，则迭代不收敛，如下图

    

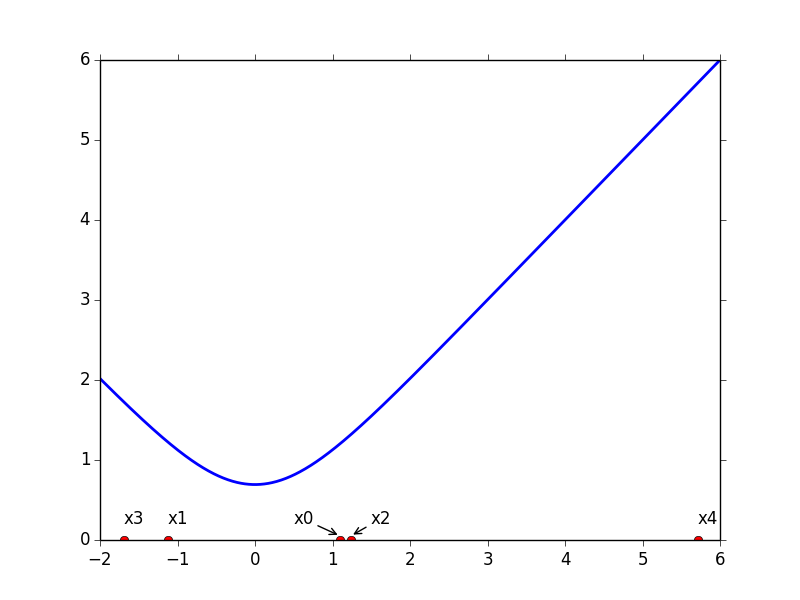
    其中 x0 到 x4 表示迭代生成的序列，可以看到，以 1.1 为初始点，迭代结果反而不断远离最优值点

    实际上 Classical Newton 是一个 locally convergent algorithm，即当初始点足够靠近最优值点时，Classical Newton 才是保证收敛的，下一节将给出证明。

Local Convergence

首先先引入 locally convergent 的概念

An iterative optimization algorithm is said to be locally convergent if for each solution $\b{x}^*$, there exists $\delta > 0$ such that for any initial point $\b{x}^0 \in B(\b{x}^*, \delta)$, the algorithm produces a sequence $\{\b{x}^k\}$ which converges to $\b{x}^*$

下面证明 Classical Newton algorithm 是 locally convergent algorithm，证明过程考虑 $x \in \mathbb{R}^1$ 的 case 即 $f: \mathbb{R} \rightarrow \mathbb{R}$，对于这个函数 Classical Newton 的迭代步骤是 $x^{k+1} = x^k - \frac{f’(x^k)}{f’‘(x^k)}$

• 证明

  假设 $f \in \mathcal{C}^3$，令 local minimum 为 $x^*$，则有

  $$x^{k+1} - x^* = x^k - x^\* - \frac{f'(x^k)}{f''(x^k)} = \frac{(x^k - x^\*)f''(x^k) - f'(x^k)}{f''(x^k)}$$

  对 $f’(x^*)$ 在点 $x^k$ 展开 truncated taylor series

  $$f'(x^*) = f'(x^k) + (x^\* - x^k)f''(x^k) + \frac{1}{2}f'''(\bar{x}^k)(x^\* - x^k)^2$$

  其中 $\bar{x}^k \in LS(x^k, x^*)$，由于 $x^*$ 是 local minimum，所以 $f’(x^*) = 0$，由此可得

  $$x^{k+1} - x^* = \frac{f'''(\bar{x}^k)}{2 f''(x^k)}(x^k - x^\*)^2$$

  等价于

  $$|x^{k+1} - x^*| = |\frac{f'''(\bar{x}^k)}{2 f''(x^k)}| (x^k - x^\*)^2$$

  如果能满足下面两个条件，则 Classical Newton 就是一个 order-two convergent algorithm

  $$\begin{align*} |\frac{f'''(\bar{x}^k)}{2 f''(x^k)}| \leq \alpha < \infty \\\\ |\frac{f'''(\bar{x}^k)}{2 f''(x^k)} (x^k - x^*)| < 1 \end{align*}$$

  第二个条件意味着 $

  x^{k+1} - x^*

  <

  x^k - x^*

  $，如果这个不等式不能成立，则无法保证算法收敛

  • 对于第一个条件

    由于 $x^*$ 为 local minimum，所以 $f’‘(x^*) > 0$，又 $f \in \mathcal{C}^3$，所以 $f’‘(x^*) \in \mathcal{C}^0$，所以

    $$\exists \eta > 0, \forall x \in (x^* - \eta, x^\* + \eta) \;\; f''(x) > 0$$

    令 $x^k \in (x^* - \eta, x^* + \eta)$，同时定义

    $$\begin{align*} \beta_1 = & \min_{x \in (x^* - \eta, x^\* + \eta)} f''(x) \\\\ \beta_2 = & \max_{x \in (x^* - \eta, x^\* + \eta)}|f'''(x)| \end{align*}$$

    (注意虽然 $f’‘(x) > 0$，但其实不用这么强的要求，只要能保证 $f’‘(x) \neq 0$ 就行了，因为它处在分母的位置，然后定义 $\beta_1 = \min_{x \in (x^* - \eta, x^* + \eta)}

    f’‘(x)

    $)

    根据上述定义，$

    \frac{f’’’(\bar{x}^k)}{2 f’‘(x^k)}

    < \frac{\beta_2}{2 \beta_1}$，这样我们就找到了第一个条件中定义的 $\alpha = \frac{\beta_2}{2 \beta_1}$

  • 对于第二个条件

    根据第一个条件有 $

    \frac{f’’’(\bar{x}^k)}{2 f’‘(x^k)} (x^k - x^*)

    < \alpha

    x^k - x^*

    < 1$，等价于

    $$x^k \in (x^* - \frac{1}{\alpha}, x^\* + \frac{1}{\alpha})$$

    即如果 $x^k$ 落在这个区间内，则条件二也满足

  在这两个条件都满足的情况下，我们有

  $$\begin{align*} & |x^{k+1} - x^*| \leq \alpha |x^k - x^\*|^2 \\\\ \Longleftrightarrow & \alpha |x^{k+1} - x^*| \leq (\alpha |x^0 - x^\*|)^{2^k} \\\\ \Longleftrightarrow & |x^{k+1} - x^*| \leq \frac{1}{\alpha} (\alpha |x^0 - x^\*|)^{2^k} \\\\ \Longleftrightarrow & \underset{k\rightarrow \infty}{\lim} |x^{k+1} - x^*| = 0 \;\; (\because \alpha |x^0 - x^\*| < 1) \\\\ \end{align*}$$

  由此我们得到如下结论

  当 $x^0 \in (x^* - \eta, x^* + \eta) \cap (x^* - \frac{1}{\alpha}, x^* + \frac{1}{\alpha})$ 时，Classical Newton 一定收敛并且是一个 order-two convergent algorithm

  虽然我们得到了在理论上可以使 Classical Newton 收敛的条件，但这个条件在实践中却是不可操作的，因为我们事先不知道 $x^*$，因此也就无法确定 $x^0$，这就在很大程度上限制了 Classical Newton 的实用性