11 - Conjugate Gradient Method
27 May 2015 Comments这篇文章的讨论基本都围绕着 quadratic function $f(\b{x}) = \frac{1}{2} \b{x}^T H \b{x} + \b{c}^T\b{x} \; (\b{x} \in \bb{R}^n)$ 进行,因为对于 conjugate gradient method,其行为在应用于 quadratic function 时最容易分析,最后会给出如何将 conjugate gradient method 应用到 non-quadratic function
下面首先会介绍 coordinate descent method 并分析其在不同情况下的收敛速度,并由此引出 conjugate gradient method,之后证明对于 quadratic function,给定 n 个 H-conjugate direction 该方法可以在至多 n 步之内收敛,然后给出 H-conjugate direction 的构建方法,最后给出 conjugate gradient method 在 non-quadratic function 上的应用
1. Coordinate Descent Method
Coordinate Descent(以下简称 CD)原理非常简单,就是每次固定 $\b{x}$ 的 $n-1$ 个维度,只针对剩下的那个维度做优化,如此迭代直到收敛为止,伪代码如下所示
CD($f(\b{x})$, $\b{x}^0$, $\epsilon$)
$k = 0$
while $\Vert \b{g}^k \Vert > \epsilon$
for $i = 1, \cdots, n$
$x_i^* = \argmin_{x_i} f(\b{x})$
$x_i = x_i^*$
$k = k+1$
return $\b{x}^k$
给定 convex, differentiable function $f(\b{x})$,CD 可以保证得到 global minimum,因为如果在每个维度上都能得到最小值,则有 $\frac{\p f(\b{x})}{\p x_i} = 0$,也就是
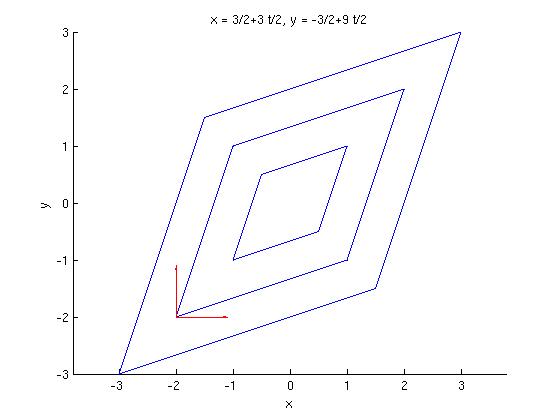
但对于 non-differentiable function,CD 就可能有问题,比如下图的情况([图片来源] (https://en.wikipedia.org/wiki/File:Nonsmooth.jpg)),可以发现在如图所示的点 无论沿着那个方向走,函数值总是变大的
下面我们观察两个 quadratic function 的例子看看 CD 在不同情况下的收敛速度,其中 $x^0 = (-1, -1)^T, \epsilon = 0.01$
-
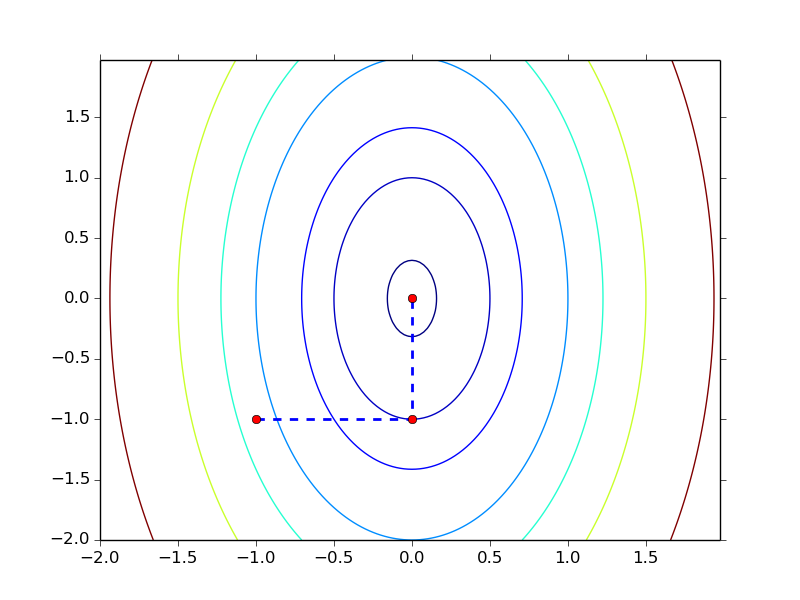
$f(\b{x}) = 4x_1^2 + x_2^2$
-
$f(\b{x}) = 4x_1^2 + x_2^2 - 2x_1x_2$
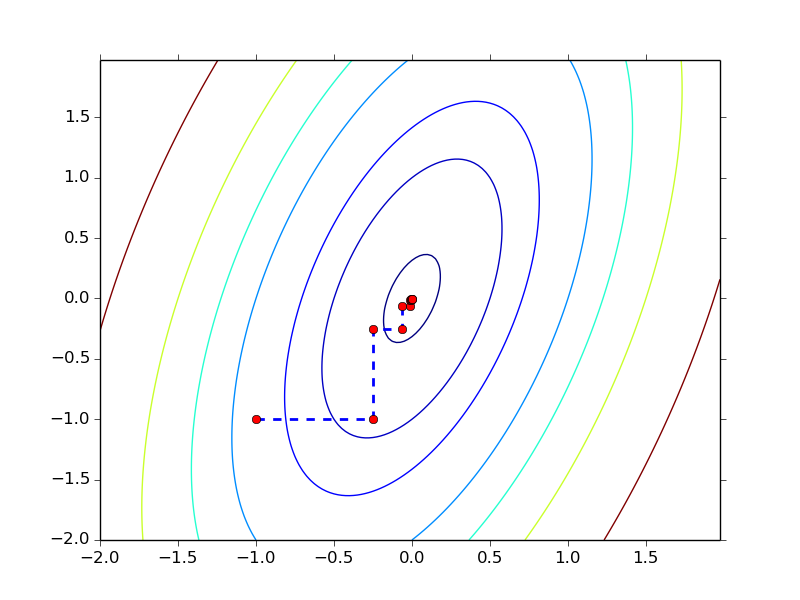
其中第一个函数用了 2 步就到达了最优点,而第二个函数用了 11 步,造成这种区别的 原因就在于 Hessian matrix,对于第一个函数,其 Hessian $\begin{pmatrix} 8 & 0 \\ 0 & 2 \end{pmatrix}$ 是一个 diagonal matrix ,而第二个函数的 Hessian $\begin{pmatrix} 8 & -2 \\ -2 & 2 \end{pmatrix}$ 则不是。Hessian 是否为 diagonal matrix 决定了函数的各个变量之间是否有相互影响, 比如第一个函数,两个变量是相互独立的,因此只要分别对两个维度各做一次优化就可以 达到 global minimum,而第二个函数则不行
2. Conjugate Gradient Method
如果我们从 descent direction 的角度来考虑,CD 相当于每一步选择 $\b{x}$ 的某一维作为 descent direction,因此前后选出的 direction 是 orthogonal 的关系。从上面的讨论中我们知道当 Hessian 为 diagonal matrix 时,这种做法可以在 n 步之内得到最优解,若 Hessian 不是 diagonal matrix 则不能
在这一节中我们将看到,通过构建 H-orthogonal (也叫 H-conjugate) direction,而不是 orthogonal direction 我们可以保证无论 Hessian 是否为 diagonal matrix,都可以在 n 步之内达到最优解,下面我们将 Conjugate Gradient Method 简称为 CG
2.1 Conjugate Direction
假设 $\b{d}^0, \b{d}^1, \cdots, \b{d}^{n-1}$ 为已知的 $n$ 个 linear independent vector,$\b{x}^0$ 为优化的初始点,则任意一个 $\b{x}$ 都可以表示为
其中 $\a^i \in \bb{R}$(把 $\b{x}^0$ 移到左边这个等式就好理解了),记 $D = (\b{d}^0, \b{d}^1, \cdots, \b{d}^{n-1})$,$\b{a} = (\a^0, \a^1, \cdots, \a^{n-1})$,则 quadratic function 可以表示为
我们可以把最后的式子看成是一个以 $\b{a}$ 为变量的 quadratic function,其 Hessian 为 $D^THD$,$(D^THD)_{ij} = {\b{d}^i}^T H\b{d}^j$,如果当 $i\neq j$ 时有 ${\b{d}^i}^TH\b{d}^j = 0$,也就是 $D^THD$ 为 diagonal matrix,那我们在这个以 $\b{a}$ 为变量的式子上应用 CD 就可以在 n 步之内得到最优解,其中第 i 步就得到 $\alpha^{i-1}$ 的最优值。如果我们把 $\b{d}^i$ 看成是 descent direction,根据公式 1,我们就相当于在 n 步之内能得到了 $\b{x}$ 的最优解
实际上,对于上面的式子,我们可以直接求解出 $\a^i$ 的具体形式
所以如果我们能找到一种方法构建 $\b{d}^0, \cdots, \b{d}^{n-1}$ 使得 ${\b{d}^i}^T H\b{d}^j = 0 \;\; \forall i \neq j$,我们就能在 n 步之内得到最优解
满足 $\b{v}^TH\b{u} = 0$ 的两个 vector 被称为 H-conjugate (或 H-orthogonal) vector
当 $H = I$ 时我们就得到了 orthogonal vector,因此 orthogonal vector 是 H-conjugate vector 的特例
Conjugate direction 是存在的,可以验证以 $H$ 的 eigenvector 作为 $\b{d}^0, \cdots, \b{d}^{n-1}$ 就可以满足 ${\b{d}^i}^T H\b{d}^j = 0 \;\; \forall i \neq j$ 的条件, 当然这种方法构建 conjugate direction 代价大了点,因此 CG 并没有用这种方法, 在后面的小节中我们会看到 CG 是怎么做的
2.2 Some Basic Properties
这一小节中列出了一些 conjugate direction 相关的一些性质
性质 1:令 $\b{g}^i$ 表示 gradient,则 ${\b{g}^i}^T\b{d}^i = {\b{g}^0}^T\b{d}^i$
-
Proof:
根据这一性质,公式 2 中定义的 $\a^i$ 实际上就是 exact line search 的结果
性质 2:${\b{g}^i}^T \b{d}^j = 0 \;\; \forall i > j$
-
Proof:
代入公式 2 可得最后一个公式等于 0,因此 ${\b{g}^i}^T \b{d}^j = 0$ $\EOP$
性质 3:$\b{d}^{0}, \cdots, \b{d}^{n-1}$ 满足 linear independent 关系
-
Proof:
性质 4:令 $\c{B}^k = \span\{ \b{d}^0, \b{d}^1, \cdots, \b{d}^{k-1} \}, \b{x}^k = \b{x}^0 + \sum_{i=0}^{k-1} \a^i \b{d}^i \;\; (k \leq n)$,则
-
Proof:
任何一个 $\b{x}^0 + \c{B}^k$ 中的点都可以表示为 $\b{x}^0 + \sum_{i=0}^{k-1} u^i \b{d}^i, u \in \bb{R}$,所以这个性质等价于
所以只要不等式 3 成立,则该性质就成立
从前面的讨论中我们知道,$\alpha^i$ 是通过 exact line search 得到的,所以有
通过展开这个不等式,可得
对该不等式从 $0$ 到 $k-1$ 做个累加就得到了不等式 3 $\EOP$
性质 4 又被成为 Expanding Subspace Theorem,它告诉我们 CG 的每一步得到的点都是 之前所有的 conjugate direction 覆盖的空间中的最优点,当 $k = n$ 时,我们就必然能得到 $\bb{R}^n$ 中的最优点
2.3 Creating Conjugate Direction
我们知道通过 Gram-Schmidt Procedure 可以将 $n$ 个 linear independent vector 转化为 orthogonal vector,其实用类似的方法我们也可以得到 H-conjugate vector, 这种方法也被称为 Conjugate Gram-Schmidt Procedure
假设存在 $n$ 个 linear independent vector $\b{v}^0, \cdots, \b{v}^{n-1}$, 我们可以按以下方法构建出 H-conjugate vector $\b{d}^0, \cdots, \b{d}^{n-1}$
- $\b{d}^0 = \b{v}^0$
- $\b{d}^i = \b{v}^i + \sum_{k=0}^{i-1} \beta^k \b{d}^k$
对于系数 $\beta$,根据 ${\b{d}^i}^T H\b{d}^j = 0 \; \forall i \neq j$,有
最后的问题就是如何得到一组 linear independent 的 $\b{v}$,答案就是用 gradient,为什么 gradient 是 linear independent 的呢?首先令 $\b{d}^0 = -\b{g}^0$(之所以有负号是因为 negative gradient 是 descent direction),根据 2.2 性质 2 ${\b{g}^1}^T \b{d}^0 = 0$,也就是 ${\b{g}^1}^T \b{g}^0 = 0$,所以 $\b{g}^1$ 和 $\b{g}^0$ linear independent, 这也就可以基于 $-\b{g}^1$ 构建 $\b{d}^1$,这样 ${\b{g}^2}^T \b{d}^1 = 0, {\b{g}^2}^T \b{d}^0 = 0$,而 $\span\{\b{g}^0, \b{g}^1\} = \span\{\b{d}^0, \b{d}^1\}$,所以 $\b{g}^2$ 和 $\b{g}^0, \b{g}^1$ 也是 linear independent 的,同理以此类推,$\b{g}^0, \cdots, \b{g}^{n-1}$ 都是 linear independent 关系(当然也有可能出现 $\b{g}^i = 0\; i < n$ 的情况,但无所谓, 因为遇到这种情况优化可以停止了,你已经到最优点了)这样就有
对于 quadratic function $f(\b{x})$,这个式子可以进一步简化。由于 $\b{x}^{i+1} = \b{x}^i + \a^i\b{d}^i$,所以 $\b{g}^{i+1} = \b{g}^i + \a^i H\b{d}^i$,这样
代入公式 4 有
根据 2.2 中的性质,上面这个公式中显然包含了很多等于 0 的项,去掉之后有
代入 $\b{d}^{i-1} = -\b{g}^{i-1} + \beta^{i-1} \b{d}^{i-1}$,最后变为
公式 5 相对于 4 简单了很多,第 $i$ 个 direction 只依赖于第 $i-1$ 个 direction 的信息,这样实现的时候保存的信息就要少很多
2.4 Algorithm
公式 3 给出了 step length 的计算公式,公式 6 给出了 descent direction 的计算公式,这样 CG 算法的核心部分都已经明确了,下面给出算法的伪代码
Input: $\b{x}^0, \epsilon$
$k = 0$
$\b{d}^0 = -\b{g}^0$
while $\Vert \b{g}^k \Vert > \epsilon$
$\a^k = -\frac{ {\b{g}^k}^T \b{d}^k}{ {\b{d}^k}^T H \b{d}^k}$
$\b{x}^{k+1} = \b{x}^k + \a^k \b{d}^k$
$\b{g}^{k+1} = H\b{x}^{k+1} + \b{c}$
$\beta^k = \frac{ {\b{g}^{k+1}}^T \b{g}^{k+1} }{ {\b{g}^k}^T \b{g}^k}$
$\b{d}^{k+1} = -\b{g}^{k+1} + \beta^k \b{d}^k$
$k = k + 1$
Output: $\b{x}^k$
下面看看 CG 在 $f(\b{x}) = 4x_1^2 + x_2^2 - 2x_1x_2$ 上的应用效果
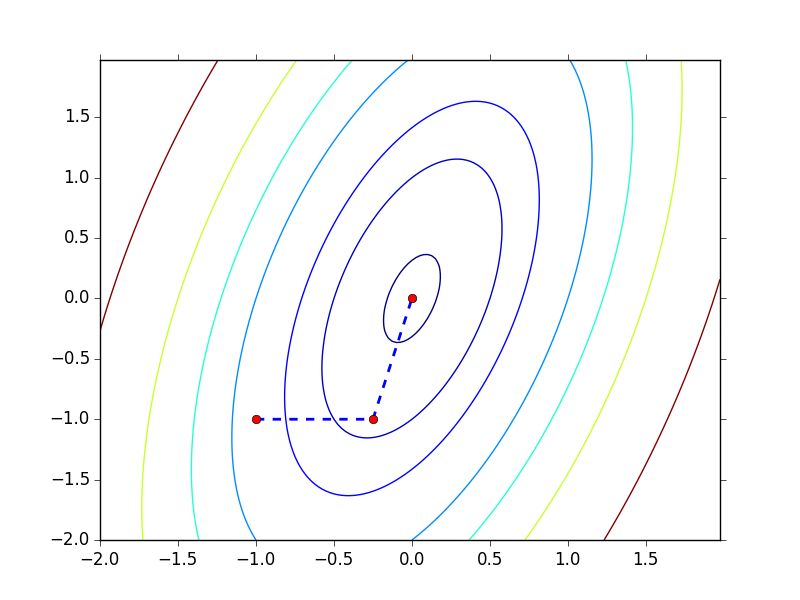
可以发现 CG 在两步之内就到达了最优点,图中的两个方向也就是 H-conjugate direction
2.5 CG for Non-quadratic Function
首先我们看看 CG 应用到 non-quadratic function 的伪代码
Input: $\b{x}^0, \epsilon$
$k = 0$
$\b{d}^0 = -\b{g}^0$
while $\Vert \b{g}^k \Vert > \epsilon$
determine $\a^k$ with line search
$\b{x}^{k+1} = \b{x}^k + \a^k \b{d}^k$
compute $\b{g}^k$
If $k < n - 1$
determine $\beta^k$
$\b{d}^{k+1} = -\b{g}^{k+1} + \beta^k \b{d}^k$
$k = k + 1$
else
$\b{x}^0 = \b{x}^{k+1}$
$\b{d}^0 = -\b{g}^{k+1}$
$k = 0$
Output: $\b{x}^k$
对比 quadratic function 的情况,主要有三个地方不同:
-
$\a^k$ 的计算
对于 non-quadratic function,很可能 exact line search 是做不到的, 因此需要其他的 line search 的方法,比如 wolfe condition 之类的
-
$\beta^k$ 的计算
由于 quadratic function 的特殊性,我们有了 $\beta^k$ 的简单形式,但由于 non-quadratic function 的复杂以及兼顾计算的方便,我们只能对 $\beta^k$ 做近似,常用的方法有 3 种
- Fletcher-Reeves method
- Polak-Ribiere method
- Hestenes-Steifel method
对比公式 6,可以发现这 3 种方法都是不同程度的近似,其中 $\beta^k_{FR}$ 其实就是 quadratic function 中使用的 $\beta^k$
关于 $\beta^k_{HS}$,它还有一点比较有意思,就是它跟 lBFGS 还能攀上点关系, 从 Quasi Newton Method 这篇笔记中我们知道
如果令 $B = I$,则 $B^k$ 就相当于 m = 1 情况下的 lBFGS 中使用的 $B^k$, 如果同时使用 exact line search,则 ${\delta^{k-1}}^T\b{g}^k = 0$,则有
可以发现 $\b{d}^{k-1}$ 前面的系数就是 $\beta^k_{HS}$
-
$\b{d}$ 的重新初始化
对应于 else 下面的那段代码。这么做是有原因的,因为对于 non-quadratic function,$\b{d}^{k+1} = -\b{g}^{k+1} + \beta^k \b{d}^k$ 并不能保证得到 descent direction,所以加上 else 下面那段代码至少保证每 n 步迭代内至少有 一步方向确实是下降的
对于 non-quadratic function,CG 对 line search 比较敏感