The Importance of Curvature (a.k.a Hessian) in Numerical Optimization

01 Oct 2014 Comments

Why Curvature Is Important

我们知道，gradient 表示函数值变化的快慢，对于函数 $f(\b{x}), \b{x} \in \mathbb{R}^n$

$$\nabla\_i f(\b{x}) = \lim\_{\varepsilon \rightarrow 0} \frac{f(x\_1, \cdots, x\_i + \varepsilon, \cdots, x\_n) - f(x\_1, \cdots, x\_i, \cdots, x\_n)}{\varepsilon}$$

表示 gradient 的第 i 个分量，$\nabla_i f(\b{x})$ 越大，函数值相对于 $x_i$ 变化越快。当 $\varepsilon$ 足够小时，上面的公式可以直接近似为 (说白了，就是一阶 taylor series)

$$\nabla\_i f(\b{x}) \approx \frac{f(x\_1, \cdots, x\_i + \varepsilon, \cdots, x\_n) - f(x\_1, \cdots, x\_i, \cdots, x\_n)}{\varepsilon}$$

假设 $\varepsilon = 0.1$ 算足够小，如果 $\nabla_i f(\b{x}) = 10$，那沿着 $x_i$ 方向走 $0.1$，函数值就差不多是下降 $1$，这里的 $\varepsilon$ 就是我们通常所说的 step length

那怎样判断给定一个 $\varepsilon$ 算不算足够小呢？对于不同的点 $\b{x}$，这个 足够小 的标准通常是不同的，对于 non-convex function 尤其如此。而这也是 curvature 发挥作用的地方

Curvature 就是以我们常说的 Hessian matrix 表示，以 $H$ 表示 Hessian matrix，$H_{ij} = \frac{\partial f}{\partial x_i \partial x_j}$，即 $f$ 在 $x_i$ 维的 gradient 随着 $x_j$ 的变化率，$H_{ij}$ 越大，这个变化就越剧烈。考虑 $H_{ii}$，$H_{ii}$ 表示 $\nabla_i f(\b{x})$ 随 $x_i$ 的变化快慢

• 如果 $H_{ii}$ 很大，$x_i$ 稍微变化一点，$\nabla_i f(\b{x})$ 就会变化很大，这样的话，$\varepsilon$ 就必须很小，因为稍微走大一点点，在 $\b{x}$ 处计算的 gradient 方向马上就失效了，函数值是上升还是下降就不好说了，因此，如果 $H_{ii}$ 很大，沿着 $x_i$ 方向就必须走得很谨慎，否则会带来优化过程的震荡

  $H_{ii}$ 很大在 function surface 上的表现就是沿 $x_i$ 方向有 valley，参考下面给出的 Rosenbrock Function

• 如果 $H_{ii}$ 很小，也就意味着 $\nabla_i f(\b{x})$ 对 $x_i$ 的变化不那么敏感，这样我就可以放心大胆得迈大步前进，不用担心 gradient 方向会很快失效，这样既加速了优化过程，又保证了函数值有足够的下降

  $H_{ii}$ 很小在 function surface 上的表现就是沿着 $x_i$ 方向特别平，极端的例子，你可以考虑平面

这里以 $H_{ii}$ 为例讨论了 curvature 信息对于优化的重要性，它决定了每一步优化的 step length (并且是每一维度的 step length) 到底多大比较合适

下面我们通过几个具体的例子看看 curvature 信息对优化过程的影响

Example 1 (one dimensional function)

首先看两个简单的一维函数

$f(x) = x^2$ $f(x) = 10 x^2$

应用 Steepest Descent + Backtrack Line Search，优化过程可以用如下两个图表示

• $f(x) = x^2$

  

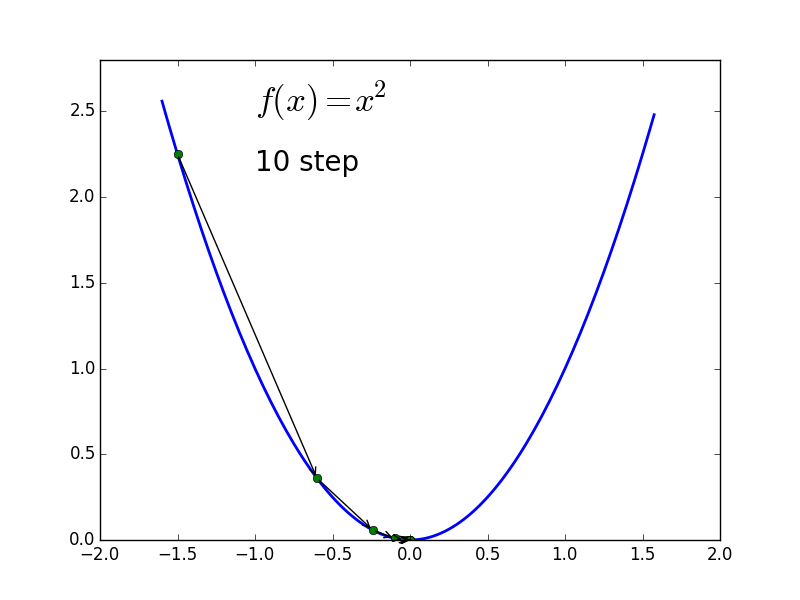
• $f(x) = 10 x^2$

  

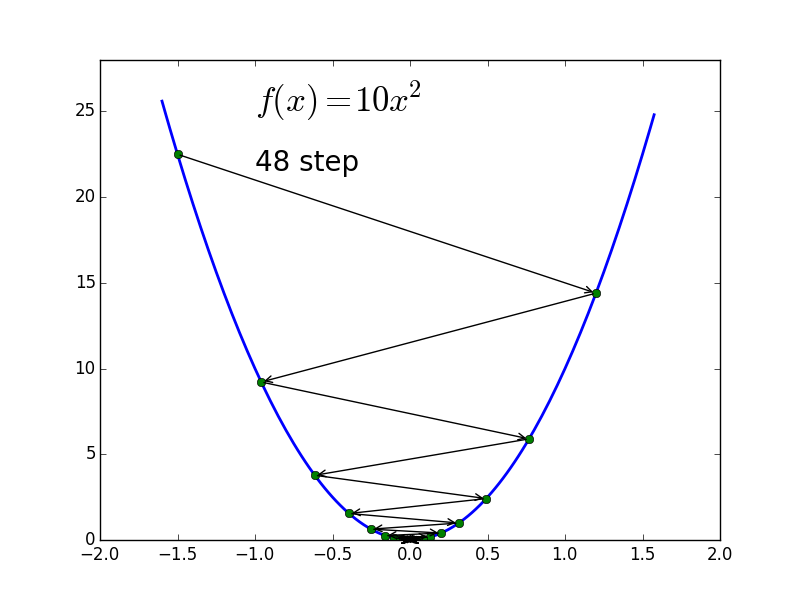
可以看到两个优化的过程都比较曲折，而其中 $f(x) = 10x^2$ 的优化过程更是左右振荡，而如果用 Newton Method 的话，根据其迭代公式

$$x^{k+1} = x^k - \frac{f'(x^k)}{f''(x^k)}$$

我们很容易发现，无论从哪里开始迭代我们都可以一步到达最优点

---

相比 Steepest Descent 的迭代步骤 (其中 $\alpha$ 表示 line search 得到的 step length)

$$x^{k+1} = x^k - \alpha f'(x^k)$$

Newton Method 实际上就是将 $\alpha$ 设置成了 $\frac{1}{f’‘(x^k)}$。另外，容易发现，当 $\alpha \gt \frac{2}{f’‘(x^k)}$ 时，迭代是发散的，$\alpha = \frac{2}{f’‘(x^k)}$ 时，迭代就一直左右震荡，所以，要想收敛，必须有 $\alpha \lt \frac{2}{f’‘(x^k)}$

Example 2 (Quadratic Programming)

假设要优化的函数为

$$f(\b{x}) = x\_1^2 + 50 x\_2^2$$

这是个很简单的 quadratic function，其对应的 $H$ 为

$$\begin{pmatrix} 2 & 0 \\\\ 0 & 100 \end{pmatrix}$$

从这个 Hessian matrix 我们可以知道

• 这个函数在所有点的 curvature 是 constant，其实对于所有的 quadratic function 这个结论都成立
• $H_{11} \neq H_{22}$，因此 $f$ 在 $x_1$ 和 $x_2$ 处 gradient 随自身的变化率是不相同的
• $H_{12} = H_{21} = 0$，因此 $x_1$ 的变化不会带来 $\frac{\partial f}{\partial x_2}$ 的变化，同样 $x_2$ 的变化也不会带来 $\frac{\partial f}{\partial x_1}$ 的变化

下面我们分别看看 Steepest Descent 和 Newton Method 应用于这个函数的结果

• Steepest Descent

  

• Newton Method

  

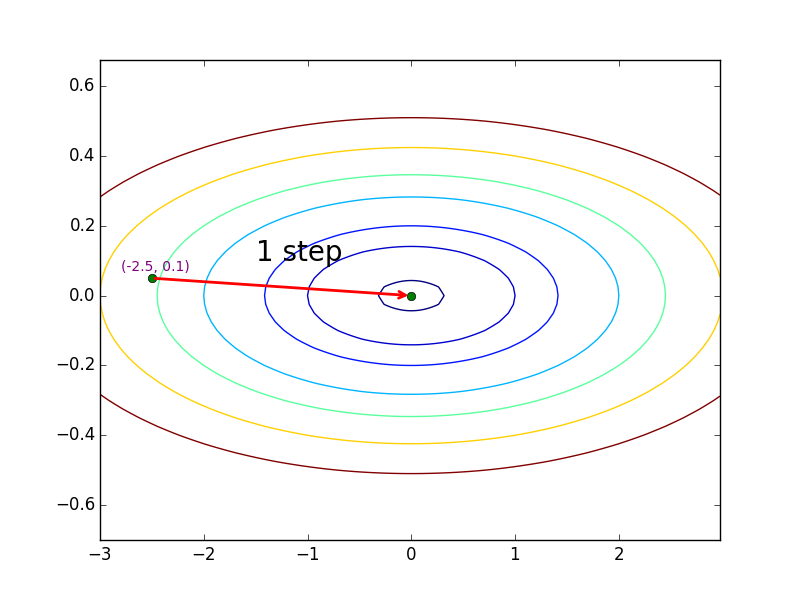
从上面的两个图可以看出，同样是从 $(-2.5, 0.1)$ 开始迭代，Steepest Descent 的迭代过程与 Classical Newton 相比要振荡得多，究其根源，就是由于 Steepest Descent 在每步选择下降方向时完全忽略 curvature 信息，而 Newton Method 则利用 curvature matrix 对下降方向进行修正。针对这个例子有

$$\b{x}^{k+1} = \b{x}^k - H^{-1} \b{g}^k = \b{x}^k - \begin{pmatrix} \frac{1}{2} & 0 \\\\ 0 & \frac{1}{100} \end{pmatrix} \b{g}^k$$

其中 $\b{g}^k$ 表示 $f$ 在 $\b{x}^k$ 处的 gradient。这么修正相当于根据 $f$ 相对于 $x_1, x_2$ 的不同的 curvature 给 $x_1, x_2$ 不同的 step length

Example 3 (Quadratic Programming)

上面的例子中，$x_1, x_2$ 的变化只影响 $f$ 相对于自身的 gradient，相互之间没有影响，下面我们看看更一般的例子，假设优化的函数为

$$f(\b{x}) = \frac{1}{2} \b{x}^T A \b{x} - \b{b}^T \b{x}$$

其中 $A$ 为 positive definite matrix。易知这里 $A$ 就是 curvature matrix

Newton Method 的迭代步骤是这样

$$\b{x}^{k+1} = \b{x}^k - A^{-1} \b{g}^k$$

其中 $\b{g}^k = A \b{x}^k - \b{b}$。这里由于 $A$ 的 off-diagonal 项不都是为 0，所以 $A^{-1}$ 不是那么好直接理解

为了便于理解，我们对 $A$ 做 eigendecomposition

$$A = Q\Lambda Q^{-1}$$

其中 $Q$ 的每一列表示 $A$ 的一个 eigenvector，由于 $A$ 是 curvature matrix，所以 $Q$ 的每一列又被称为 curvature axis，如下图所示，其中长的那个 axis 对应 eigenvalue 最大的 eigenvector，该 eigenvector 被称为 principal eigenvector，也是 curvature 最大的方向

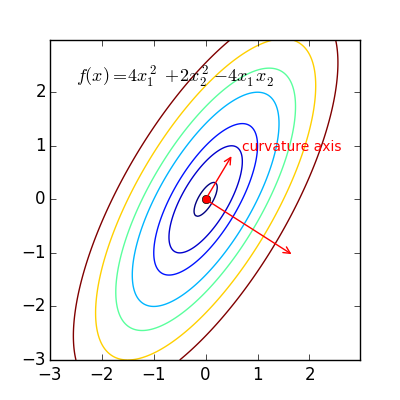
$\Lambda$ 是一个 diagonal matrix，对角线上每一项都表示 $A$ 的 eigenvalue，也就是 $f$ 沿 curvature axis 的 curvature。有了这个 decomposition 结果，我们可以对上述迭代做如下变换

$$\begin{align*} & \b{x}^{k+1} = \b{x}^k - Q\Lambda^{-1}Q^{-1} \b{g}^k \\\\ \Longleftrightarrow & Q^{-1} \b{x}^{k+1} = Q^{-1} \b{x}^k - \Lambda^{-1} (Q^{-1} \b{g}^k) \end{align*}$$

$Q$ 的列向量构成 eigenspace，对于原空间中的任何一个变量 $\b{v}$，$Q^{-1}\b{v}$ 表示 $\b{v}$ 在 eigenspace 中的新坐标，因此如果把 Newton Method 的迭代映射到 eigenspace 中理解，它的效果就跟上个例子中的迭代一样，其实对于上一个例子，$Q = I$，eigenspace 和原空间是同一个空间

---

结合 Example 1 中对 1d function 的 step length 的讨论，我们也可以得出对于 quadratic programming step length 的限制

以 $\lambda_{max}$ 表示最大的 eigenvalue，则 step length 一定不能超过 $\frac{2}{\lambda_{max}}$，否则迭代在 principal eigenvector 方向是发散的，从而整个迭代就不能收敛。当 step length $= \frac{1}{\lambda_{max}}$ 时，迭代在 principal eigenvector 方向收敛是最快的，但可能造成其他方向上收敛较慢

Example 4 (Rosenbrock Function)

Rosenbrock function 在接近 local minimum 的地方有个很深的 valley，如下图所示 (image from here)

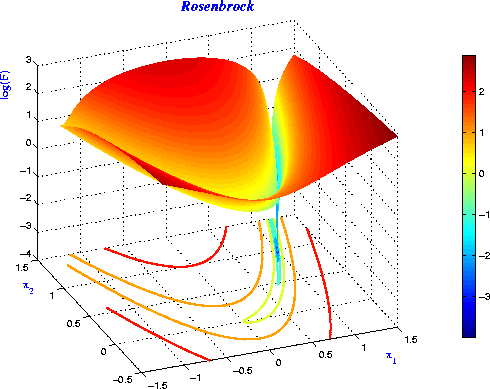
函数的 surface 上的 valley 就是 curvature 比较大的地方。对比 steepest descent 和 classical newton 中关于 Rosenbrock 的例子，可以发现 steepest descent 在 valley 处花费了很大力气才最后走到 local minimum，而 Newton method 由于考虑了 curvature 信息要快非常多

Conclusion

综上所述，优化过程需要把 curvature 考虑进去才能有更好的收敛性能

现实中，通常由于计算资源的限制，我们不能使用完整的 curvature 信息。为此，优化专家们发明了各种各样的方法去做近似，比如

• BFGS (L-BFGS)，一种十分常用的优化算法
• Gradient Descent 中用到的 momentum 也可以看作一种对 curvature 信息的简单近似，因为它将历史上 gradient 的变化考虑了进去
• Hessian-free for deep learning